Certifiably Optimal Anisotropic Rotation Averaging

Carl Olsson, Yaroslava Lochman, Johan Malmport, and Christopher Zach

code · arxiv

Abstract

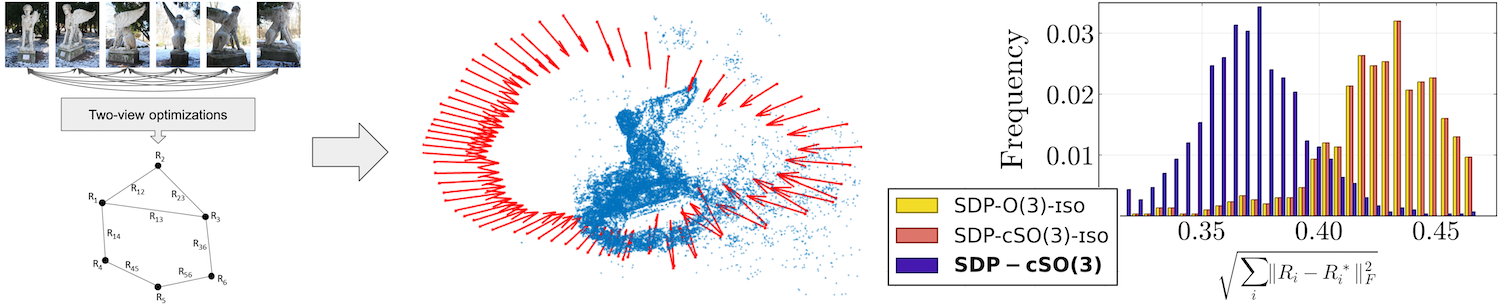
Rotation averaging is a key subproblem in applications of computer vision and robotics. Many methods for solving this problem exist, and there are also several theoretical results analyzing difficulty and optimality. However, one aspect that most of these have in common is a focus on the isotropic setting, where the intrinsic uncertainties in the measurements are not fully incorporated into the resulting optimization task. Recent empirical results suggest that moving to an anisotropic framework, where these uncertainties are explicitly included, can result in an improvement of solution quality. However, global optimization for rotation averaging has remained a challenge in this scenario. In this paper we show how anisotropic costs can be incorporated in certifiably optimal rotation averaging. We also demonstrate how existing solvers, designed for isotropic situations, fail in the anisotropic setting. Finally, we propose a stronger relaxation and show empirically that it is able to recover global optima in all tested datasets and leads to a more accurate reconstruction in all but one of the scenes.

Citation

@article{olsson2025certifiably,
    author    = {Olsson, Carl and Lochman, Yaroslava and Malmport, Johan and Zach, Christopher},
    title     = {Certifiably Optimal Anisotropic Rotation Averaging},
    journal   = {arXiv preprint arXiv:2503.07353},
    year      = {2025},
}