ACD. Making Rotation Averaging Fast and Robust with Anisotropic Coordinate Descent
Yaroslava Lochman, Carl Olsson, and Christopher Zach
BMVC 2025
code (julia) · paper · paper+supplementary · poster · short presentation
Abstract
Anisotropic rotation averaging has recently been explored as a natural extension of respective isotropic methods. In the anisotropic formulation, uncertainties of the estimated relative rotations—obtained via standard two-view optimization—are propagated to the optimization of absolute rotations. The resulting semidefinite relaxations are able to recover global minima but scale poorly with the problem size. Local methods are fast and also admit robust estimation but are sensitive to initialization. They usually employ minimum spanning trees and therefore suffer from drift accumulation and can get trapped in poor local minima. In this paper, we attempt to bridge the gap between optimality, robustness and efficiency of anisotropic rotation averaging. We analyze a family of block coordinate descent methods initially proposed to optimize the standard chordal distances, and derive a much simpler formulation and an anisotropic extension obtaining a fast general solver. We integrate this solver into the extended anisotropic large-scale robust rotation averaging pipeline. The resulting algorithm achieves state-of-the-art performance on public structure-from-motion datasets.
Pseudo-code
Input: relative rotations Rrel (Rrel_ij ≈ R_j @ R_i.T), corresponding Hessians H.
Output: absolute rotations R.
R = initialize_rotations(n) # R is nx3x3
N = construct_cost_matrix(Rrel, H) # N is nxnx3x3
# N[i,j] =
# (tr(H_ij)/2 I − H_ij) @ Rrel_ij
# if Rrel_ij exists
# 0 otherwise
for iter in range(max_iter):
for k in shuffle([1,...,n]):
R[k] = project_on_SO3(sum(bmm(N[k].transpose(2,3), R), axis=1))
if converged:
break
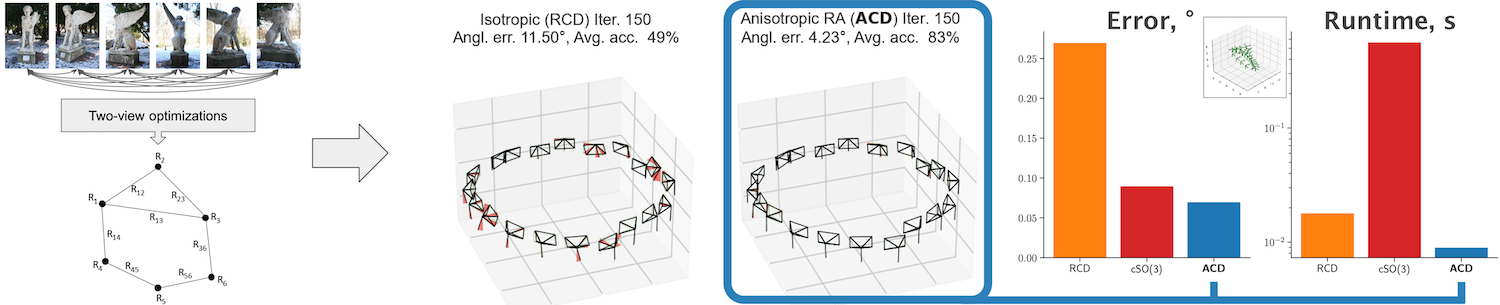
Comparison with isotropic rotation averaging
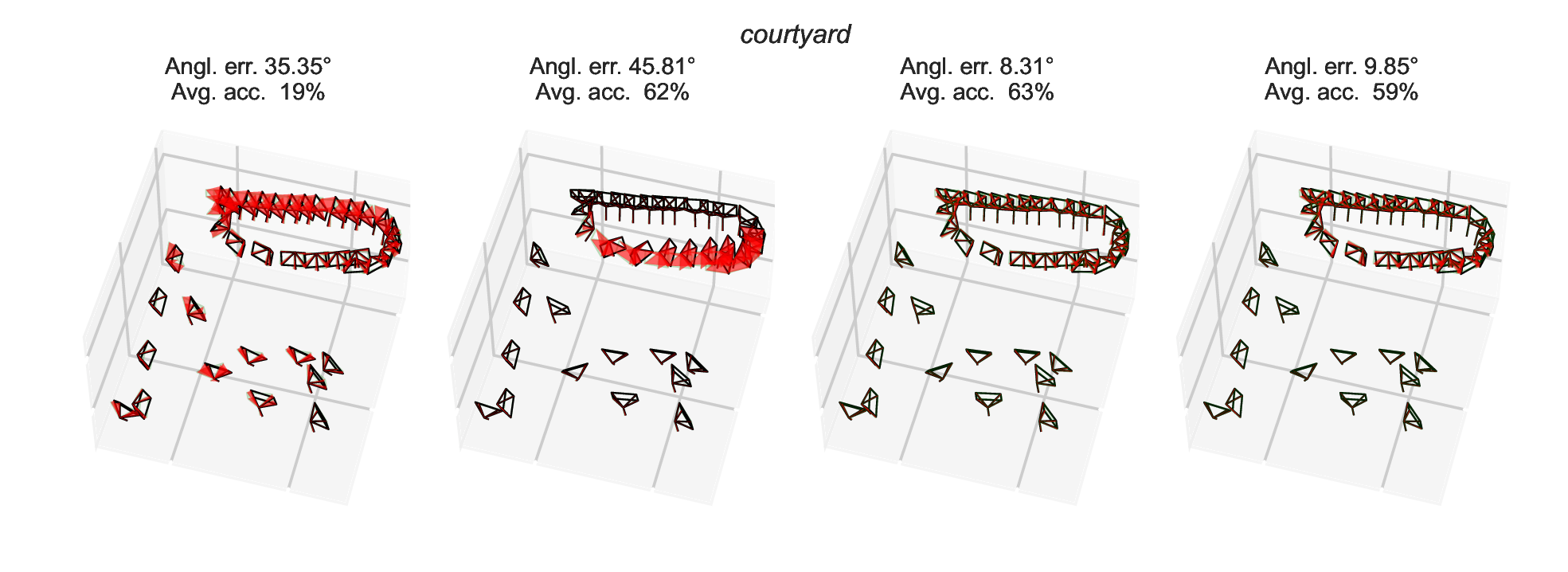
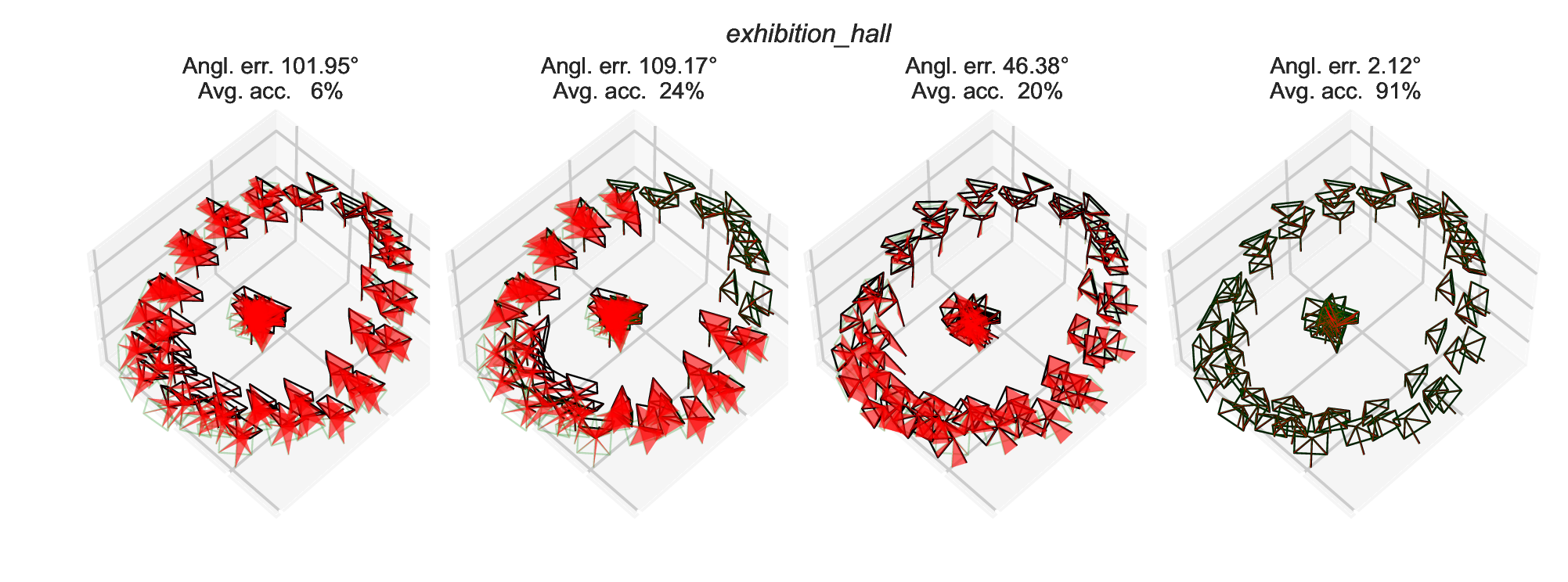
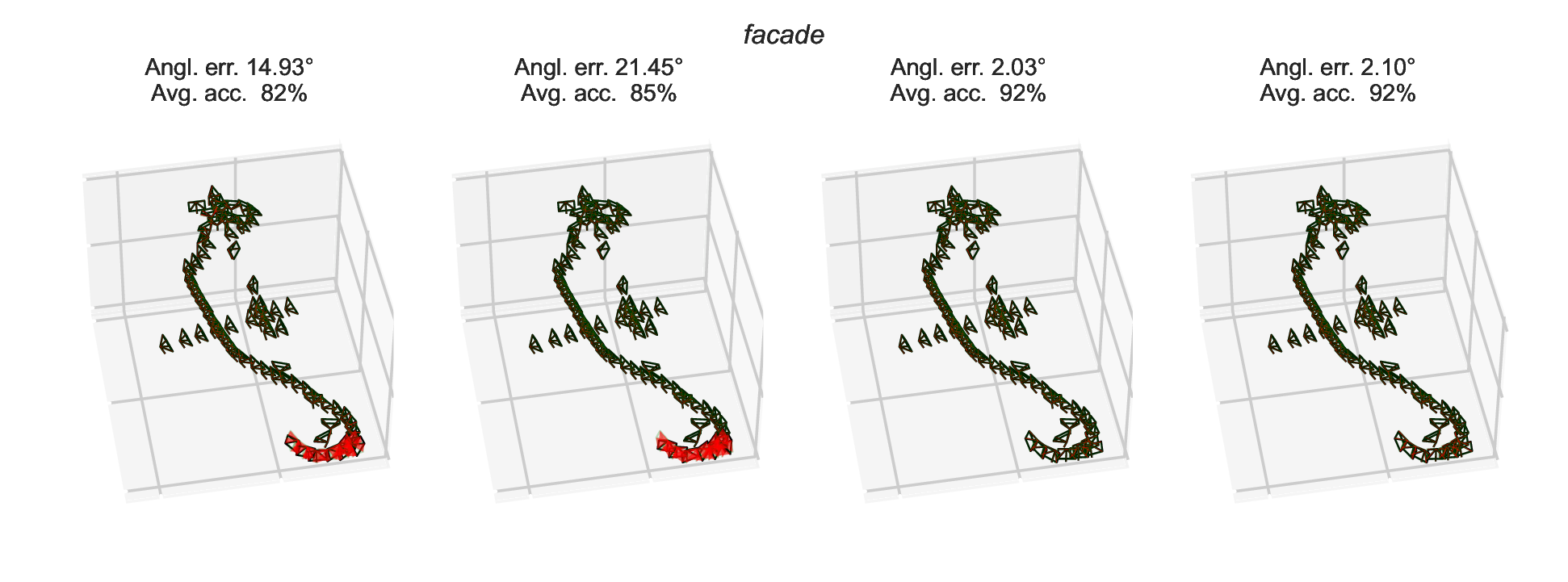
ETH3D MVS reconstructions
We run the two-view reconstruction pipeline on ETH3D datasets using SIFT keypoints and minimal filtering (based on cheirality only). The obtained relative rotations are very noisy and contain outliers. Some reconstructions are shown below, where deviations from ground truth are highlighted in red.
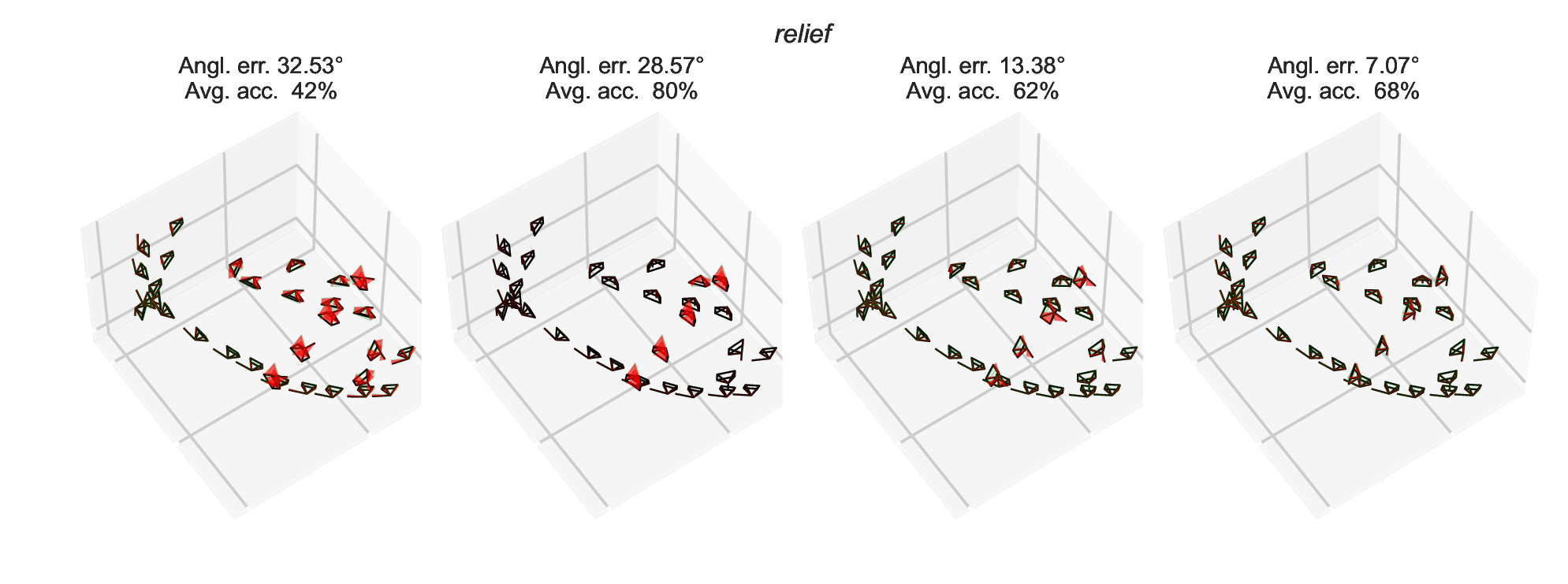
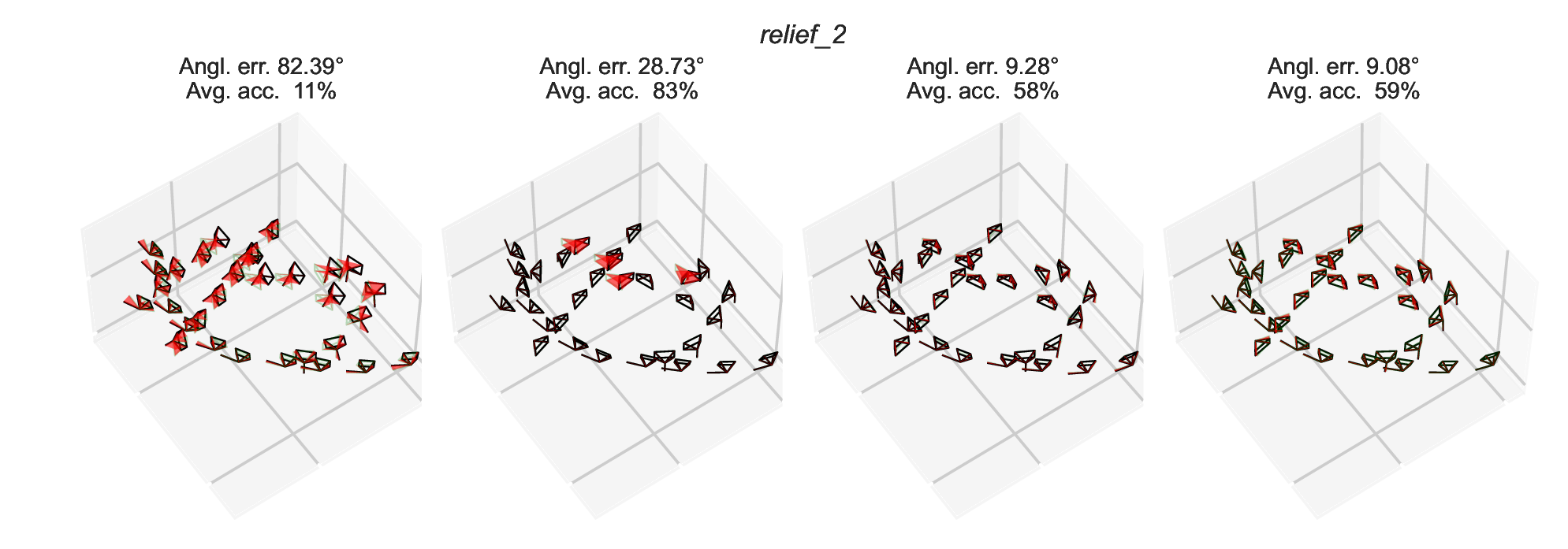
BibTeX
@article{lochman2025making,
author = {Yaroslava Lochman and Carl Olsson and Christopher Zach},
title = {Making Rotation Averaging Fast and Robust with Anisotropic Coordinate Descent},
booktitle = {36th British Machine Vision Conference 2025, {BMVC} 2025, Sheffield, UK, November 24-27, 2025},
publisher = {BMVA},
year = {2025},
url = {https://bmva-archive.org.uk/bmvc/2025/assets/papers/Paper_516/paper.pdf}
}